Digital Logic in Python
The goal that I started with was to be able to express a 8-bit full adder in Python. The outcome of this as to be able to then output this representation to different formats.
The motivation for this was after trying to model logic circuit in a software package that had an automation system like Node-RED. It was very time consuming and it required remembering which parts gates of the different components needed hooking up, which resulted in errors.
Out of this my digital package was born.
Key Classes
- Input - Represents the input of a gate, it has an output which is populated when it is set with a value. This is used to seed the system with data. It can be thought of as defining the function parameters.
- BinaryGate - A binary gate takes two inputs and produces one output.
- AndGate
- OrGate
- NorGate
- XorGate
With those primitives, I could then build a full adder. A full adder has three inputs a, b and the carry_in and two outputs the sum and the carry out.
The following is first pass version focusing on the guts of the component. The later implementation supported optionally taking in the three inputs so you could source them from other components.
class FullAdder:
def __init__(self):
# Inputs
self.a = Input('a')
self.b = Input('b')
self.carry_in = Input('carry_in')
# In between.
c = XorGate(self.a, self.b)
d = AndGate(c, self.carry_in)
e = AndGate(self.a, self.b)
# Outputs
self.carry_out = OrGate(d, e)
self.sum = XorGate(c, self.carry_in)
When chaining two full adder's together, you connect the carry_out of the
previous one to the carry_in of the next. The system I put together allows the
carry_out of one FullAdder to be passed in as the carry_in of another. This is
achieved with the following:
```python
class FullAdder:
def __init__(self, a=None, b=None, carry_in=None):
# Inputs
self.a = a or Input('a')
self.b = b or Input('b')
self.carry_in = carry_in or Input('carry_in')
...
The next part was create a FullAdder that uses a universal logic gate such as NOR.
class FullAdderNorOnly:
"""A full adder using only NOR (a universal logic gate)."""
def __init__(self, a=None, b=None, carry_in=None):
# Inputs
self.a = a or Input('a')
self.b = b or Input('b')
self.carry_in = carry_in or Input('carry_in')
# In between.
c = NorGate(self.a, self.b)
f = NorGate(NorGate(self.a, c), NorGate(c, self.b))
g = NorGate(self.carry_in, f)
# Outputs
self.carry_out = NorGate(c, g)
self.sum = NorGate(NorGate(f, g), NorGate(g, self.carry_in))
In addition to being able to configure the components as seen so far, I also wanted to make sure that it was possible to evaluate the gates to confirm they were giving the right output. As such the gates support the call operator.
class AndGate(BinaryGate):
"""And gate has two inputs and one output.
It returns true only if both inputs are true.
"""
def __call__(self, a, b):
return bool(a and b)
class OrGate(BinaryGate):
"""Or gate has two inputs and one output.
It returns true if at least one input is true.
"""
def __call__(self, a, b):
return bool(a or b)
You may notice something slightly off here is the operator doesn’t depend on the instance itself (i.e there is no self here). This was mostly done so that function was straight forward and simple and instead there is machinery behind the scenes that handles propagating the values and calling the gates with the appropriate inputs for them.
A sneak peak of how this works for binary gates such as the AND and OR gates shown above is:
class BinaryGate:
...
def eval(self):
if self.a.output is not None and self.b.output is not None:
self.output = self(self.a.output, self.b.output)
for callback in self.callbacks:
callback.eval()
After checking the inputs have value (i.e are not None), it then calls it to compute the result followed by calling the other callbacks. Callbacks maintains a list of the other gates/components that are depending on the current gate.
For example, using the full adder shown before the OrGate that represents the
carry-out will be evaluated once the two AndGate instances has its output.
Once the basics were sorted I set out to make a Adder8BitUniversal which is
an -8-bit adder using only NOR gates.
Another component I built for testing and development was IntegerToBinary
which handles going from an integer of a certain bit length and converting it
to an array of booleans and in the case of the system, it defines 1-bit outputs
that can be used as the input other components (i.e NorGate or at the higher
level the Adder8BitUniversal.
I realised the system was quite generic enough that it wasn’t much effort to create a AddrNBit which could be used to generate an 8-bit adder, 16-bit or 32-bit adder, so I set that up.
Graphing / Visualising
The original goal of the system was not to only model the circuits in Python but to be able take their definition and produce elsewhere.
This is where there Visitor class comes into play as it handles visiting
each component to give you an opportunity to describe it for another system.
The system I will show here is GraphViz or DOT language.
The function for producing a GraphViz graph actually makes use of two visitors, by performing two passes over it. The first handles all the nodes (gates) and the second all the edges (connections).
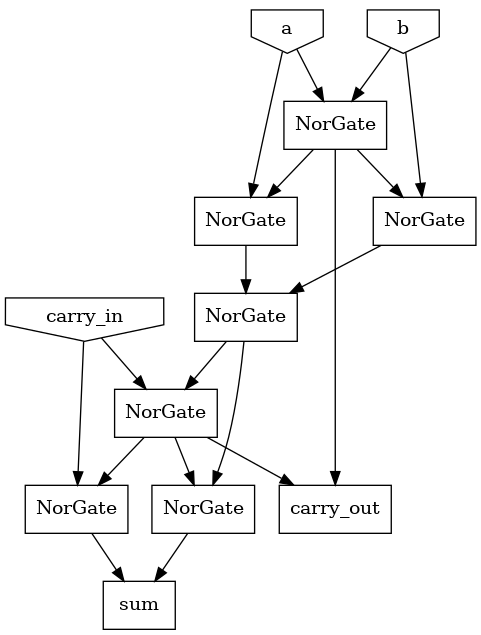
This proved very useful as I was indeed able to quickly jump from 8-bit full adder to a 16-bit full adder with very minimal changes.
Future
There were three additional backends that I had considered writing and even started a little.
- Skia - This would involve implementing my own layout engine which I’ve been meaning to do for quite some time. The University of Adelaide set that as one of the assignments after I left. Perhaps best saved for a time where I decide to go Skia and Graph and eliminate the specifics of this digital logic project.
- Virtual Machine - This is really a bigger project in itself which was create virtual machine for digital logic. I’ve started working on this, but haven’t gotten to the stage where its implemented. If I do continue this and get it to a workable state, I will post about it.
- LLVM - The basic idea was to generate LLVM IR that is runnable via lli.